Question

Suppose that diastolic blood pressure readings of adult males have a bell-shaped distribution with a mean of 82 mmHg and a standard deviation of 10 mmHg. Usingthe empirical rule, what percentage of adult males have diastolic blood pressure readings that are at least 62 mmHg? Please do not round your answer.

Answer 1

We will use the 68-95-99.7 rule.

We have a bell-shaped distributed data with mean 82 mmHg and standard deviation of 10 mmHg.

We have to estimate the percentage of adult males that have diastolic blood pressure that are at least 62 mmHg.

We start by estimating how many standard deviations is 62 mmHg from the mean.

This can be done calculating the z-score:

`\begin{gathered} z=(X-\mu)/(\sigma) \\ z=(62-82)/(10) \\ z=-(20)/(10) \\ z=-2 \end{gathered}`

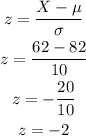
So 62 mmHg is 2 standards deviation below the mean.

We know, from the empirical rule, that 95% of the data is within 2 standards deviation of the mean (to both sides).

Then, we can estimate that 95/2% = 47.5% of the data is between 62 mmHg and the mean (82 mmHg).

Also, we know that 50% of the data will be above the mean.

Then, we can graph the amount of data that is above 62 mmHg as:

Then, the percentage of data above 62 mmHg is:

`47.5\%+50\%=97.5\%`

Answer: 97.5% of the adult males are expected to have diastolic blood pressure readings that are at least 62 mmHg.