Question

A kite 100ft above the ground moves horizontally at a speed of 8ft/s. At what rate is the angle between the string and the horizontal decreasing when 200ft of string has been let out?

Answer 1

so hmm notice the picture

at the moment r = 200, or the string is 200ft to the kite up above, at that moment, those are the values for "x" and θ

however, "r" has a rate, so.. we wont' be using that one to get the angle, we'll use the "constant y" or 100

thus
`\bf tan(\theta)=\cfrac{100}{x}\implies tan(\theta)=100x^(-1)\\\\ -----------------------------\\\\ sec^2(\theta)\cfrac{d\theta}{dt}=-\cfrac{100}{x^2}\cdot \cfrac{dx}{dt}\implies \cfrac{1}{cos^2(\theta)}\cdot\cfrac{d\theta}{dt}=-\cfrac{100}{x^2}\cdot \cfrac{dx}{dt} \\\\\\ \cfrac{d\theta}{dt}=\cfrac{-cos^2(\theta)\cdot 100\cdot (dx)/(dt)}{x^2}`

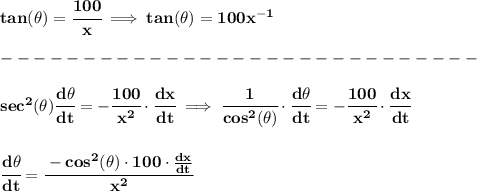
so hmm, pretty sure you can take from there, keeping in mind that dx/dt is 8