Question

the diameter of a parabolic mirror is 22 centimeters and the mirror has a depth of 0.5 centimeter at th center what is the equation of the cross sectional parabola of the mirror.

Answer 1

I figured it out
warning: mildly incoherent math logic ahead


ok, so if you want a parabola facing right, then
first I'll solve for up down standard parabola then reflect across x=y line
so
y=ax²+bx+c

so let's say teh vertex is at the origin
that means when x=0, y=0
0=0
c=0
y=ax²+bx
ok, see diagram
we have some points, (0,0) and (11,0.5) and (-11,0.5)
use those oints to find a and b
0.5=121a+11b
0.5=121a-11b
add dem equations
1=242a
divide by 242
1/242=a
subsitute
0.5=121a+11b
0.5=121(1/242)+11b
0.5=0.5+11b
0=11b
0=b
oook

de equaiton is

`y= (1)/(242) x^2`
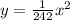
if we want it facing right
switch x and y

`x= (1)/(242) y^2`



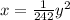
the equation is
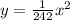
`y= (1)/(242) x^2` or
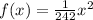
`f(x)= (1)/(242) x^2` or
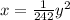
`x= (1)/(242) y^2` or
`f(y)= (1)/(242) y^2`
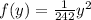
depends which way you want it and if you want f(x) or f(y) or x or y