Answer:
Explanation:
Alright, lets get started.
Equation is : F = mg sinΘ
We have given,
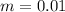
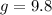
Θ
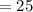
While plugging these above values in equation:
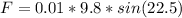
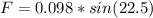
Now, if we look unit circle, we don't have angle 22.5, so we will use half angle identity
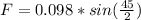
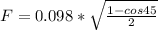
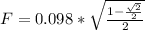
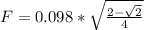
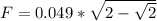 : Answer
: Answer
Hope it will help :)