Question

given a can of 3 tennis balls. no room on the top, bottom, or sides. one measurement is given of height 8.25. To the nearest tenth how much of a cubic inch what is the volume of air. imagine the can is a perfect cylinder

Answer 1

Since there is no room on the top, bottom or sides, the radius of the ball is equivalent to the radius of the cylinder, and also the height of the cylinder is equivalent to the length of 6 times the radius of the ball (three balls, each one with two radii).

So the value of the radius is:

`\begin{gathered} 6r=8.25 \\ r=(8.25)/(6) \\ r=1.375 \end{gathered}`

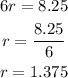
Now, we can calculate the volume of the cylinder using the formula:

`\begin{gathered} V=\pi r^2h \\ V=\pi\cdot1.375^2\cdot8.25 \\ V=49 \end{gathered}`

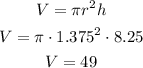
The volume of the three balls is given by:

`\begin{gathered} V=3\cdot((4)/(3)\pi r^3) \\ V=4\cdot\pi\cdot1.375^3 \\ V=32.67 \end{gathered}`

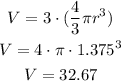
Now, subtracting these volumes, we have the volume of air:

`49-32.67=16.33`

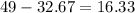
Rounding to the nearest tenth, the volume of air is 16.3 in³.