Question

The quadratic function f(x) = –x2 – 6x – 8 is graphed. What are the solutions of the quadratic equation 0 = –x2 – 6x – 8?

Answer 1

-x^2-6x-8=0

-x^2-2x-4x-8=0

-x(x+2)-4(x+2)=0

(-x-4)(x+2)=0

-(x+4)(x+2)=0

x=-4, -2 so the two solutions are the points (-4, 0), (-2, 0)

Answer 2

Explanation:

Hi there, every time we pick a function and instead of f(x) we place a 0. We've just turned it into an equation.

So that's the case.

`0=-x^(2) -6x-8\\ x^(2) +6x+8=0\\`

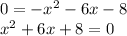
As a=1, then the solution may also be found through another method. Which two numbers and their product is 8? And the same two number added gives us 6?

`P(x)=4*2=8\\ S(x)=4+2=6\\`

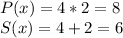
As their opposite numbers to 4 and 2 so the Solution Set is

S={-4,-2}

We could find the solution through the Quadratic Formula as well

`(6+√(36-4(-1)(-8)))/(2*(-1))\\(6-2)/(-2)=-2 ,(6+2)/(-2)=-4`

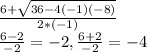
S={-4,-2}