Answer:
refer attachment for the graph.
Explanation:
Given: The equation
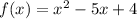
We have to draw the the graph for the given equation.
Consider the given equation
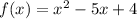
The vertex of the parabola of the form
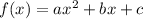 is given by
is given by
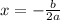
Here, a = 1 , b = -5 and c = 4
Thus, vertex is
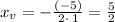
Also, the y coordinate at
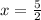 is
is
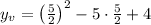
Simplify, we get,
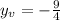
Thus, The vertex of parabola is
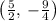
y - intercept is the point where x = 0
Plug x = 0 in given equation
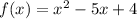
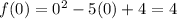
Thus, y - intercept is (0,4)
Now, we calculate x- intercept
x- intercept is where y is equal to 0.
Put f(x) = 0
We have,

Solving the given quadratic equation using quadratic formula ,we have
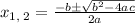
we have a = 1 , b = -5 and c = 4

Simplify, we have,
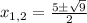
Thus,

Thus, The x - intercept are (4,0) and (0,1)
Plot the graph and we obtain as shown below.