Question

a cyclist pedaling at a steady rate travels 30 miles with the wind. He can travel only 18 miles against the wind in the same amount of time. If the rate of the wind is 3 mph, what is the cyclist's rate without the wind?

Answer 1

so.. traveling without the wind, let's say the pedalist has a speed of "r"

with the wind, the wind's rate is added to it, so, he's not going "r" fast, he's really going r+3 fast

against the wind, he's going r - 3 fast

notice, he covers 30 miles with it, and 18 miles against BUT the time for both ways is the same, say time "t"

now, recall your d = rt, distance = rate * time

thus
`\bf \begin{array}{lccclll} &distance(mi)&rate(mph)&time\\ &-----&-----&-----\\ \textit{with the wind}&30&r+3&t\\ \textit{against the wind}&18&r-3&t \end{array}\\\\ -----------------------------\\\\ \begin{cases} 30=(r+3)t\implies (30)/(r+3)=t\\\\ 18=(r-3)t\implies (18)/(r-3)=t \end{cases}\implies t=t\implies \cfrac{30}{r+3}=\cfrac{18}{r-3}`

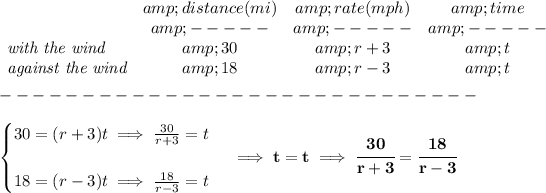
solve for "r"