Question

Use mathematical induction to prove that the statement is true for every positive integer n. 8 + 16 + 24 + . . . + 8n = 4n(n + 1)

Answer 1

First show the statement holds for
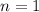
`n=1`. The left hand side is just 8, and the right hand side is
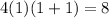
`4(1)(1+1)=8`, so it's true.

Assume the statement holds for
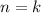
`n=k`, i.e.


`8+16+\cdots+8(k-1)+8k=4k(k+1)`

and use this to show it holds for
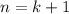
`n=k+1`, i.e.


`8+16+\cdots+8(k-1)+8k+8(k+1)=4(k+1)(k+2)`

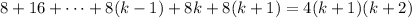
By the assumption above, you have


`\underbrace{8+16+\cdots+8(k-1)+8k}_(n=k)+8(k+1)=4k(k+1)+8(k+1)=4(k+1)(k+2)`

so the statement is true for all
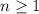
`n\ge1`.