Question

Which function represents a reflection of ƒ(x) = 2x?

h(x) = 2^x + 1
h(x) = 2^x - 1
h(x) = 2^x - 1
h(x) = 2^-x

Answer 1

a reflection across the x axis means times the whole thing by -1
reflect across y axis means multiply every x by -1

so we got
from f(x)=2x
a reflection across either axis results in f(x)=-2x
but wat
why we have exponents

I pick the last option, h(x)=2^-x

Answer 2

Answer:
`h(x) = 2^(-x)`

Explanation:

Here the given function is,

`f(x) = 2^x`

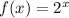
Let (x,y) are the coordinates of the above exponential function,

By the rule of reflection about x-axis,

`(x,y)\rightarrow (-x,-y)`

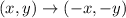
Thus, in the transformed figure that is obtained after the reflection about x-axis,

x is replaced by -x and y is replaced by -y,

Let h(x) = - f(x)

Hence, the transformed figure is,

`h(x) = 2^(-x)`

⇒ Last Option is correct.