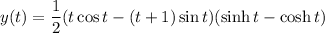Question

Question on laplace transform... number 7

Answer 1

Recall a few known results involving the Laplace transform. Given a function
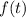
`f(t)`, if the transform exists, then denote it by
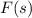
`F(s)`. We have


`\mathcal L_s\left\{e^(ct)f(t)\right\}=\mathcal L_(s-c)\left\{f(t)\right\}=F(s-c)`


`\mathcal L_s\left\{\displaystyle\int_0^t f(u)\,\mathrm du\right\}=\frac{F(s)}s`


`\mathcal L_s\left\{f'(t)\right\}=sF(s)-f(0)`

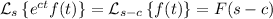
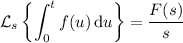
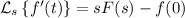
Let's put all this together by taking the transform of both sides of the ODE:


`y'(t)+2e^(-2t)\displaystyle\int_0^te^(2u)y(u)\,\mathrm du=e^(-t)\sin t`


`\implies \bigg(sY(s)-y(0)\bigg)+2\mathcal L_s\left\{e^(-2t)\displaystyle\int_0^te^(2u)y(u)\,\mathrm du\right\}=\frac1{(s+1)^2+1}`

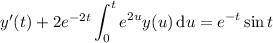
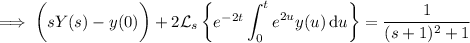
Here we use the third fact and immediately compute the transform of the right hand side (I'll leave that up to you).

Now we invoke the first listed fact:


`\mathcal L_s\left\{e^(-2t)\displaystyle\int_0^te^(2u)y(u)\,\mathrm du\right\}=\mathcal L_(s+2)\left\{\displaystyle\int_0^te^(2u)y(u)\,\mathrm du\right\}`

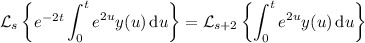
Let
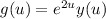
`g(u)=e^(2u)y(u)`. From the second fact, we get


`\mathcal L_s\left\{\displaystyle\int_0^tg(u)\,\mathrm du\right\}=\frac{G(s)}s\implies\mathcal L_(s+2)\left\{\displaystyle\int_0^tg(u)\,\mathrm du\right\}=(G(s+2))/(s+2)`

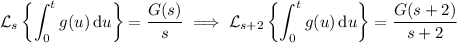
From the first fact, we get


`G(s)=\mathcal L_s\left\{e^(2u)y(u)\right\}=Y(s-2)`

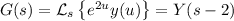
so we're left with


`(G(s+2))/(s+2)=(Y((s+2)-2))/(s+2)=(Y(s))/(s+2)`

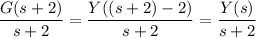
To summarize, taking the Laplace transform of both sides of the ODE yields


`sY(s)+(2Y(s))/(s+2)=\frac1{(s+1)^2+1}`

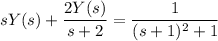
Isolating
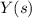
`Y(s)` gives


`Y(s)=\frac1{\left(s+\frac2{s+2}\right)\left((s+1)^2+1\right)}`

`Y(s)=(s+2)/(\left((s+1)^2+1\right)^2)`

All that's left is to take the inverse transform. I'll leave that to you as well. You should end up with something resembling


`y(t)=\frac12(t\cos t-(t+1)\sin t)(\sinh t-\cosh t)`