Question

According to the Rational Root Theorem, the following are potential roots of f(x) = 60x2 – 57x – 18

-6/5, -1/4, 3, 6
Which is an actual root of f(x)?

-6/5
-1/4
3
6

Answer 1

We have been given the function
`f(x) = 60x^2 - 57x -18`

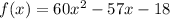
Now, the given potential roots are -6/5, -1/4, 3, 6. In order to find the actual root of this function, we substitute the root in the given function and if we get zero, then that would be the actual zero.

`f(-6/5)=60(-6/5)^2-55\cdot(-6)/(5) -18= (684)/(5)\\eq 0\\\\f(-1/4)=60(-1/4)^2-55\cdot(-1)/(4) -18=0\\\\\\f(3)=60(3)^2-57(3)-18=351\\eq 0\\\\f(6)=60(6)^2-57(6)-18=1800\\eq 0`

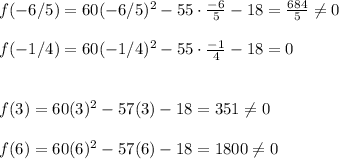
We got zero for the value -1/4.

Hence, the actual root of f(x) is -1/4.

B is the correct option.