Question

According to the Rational Root Theorem, which could be a factor of the polynomial f(x) = 6x4 – 21x3 – 4x2 + 24x – 35?

a. 2x – 7
b. 2x + 7
c. 3x – 7
d. 3x + 7

Answer 1

the answer is the first option, A) 2x-7

Answer 2

Answer with explanation:

The given Polynomial function is

`f(x)= 6x^4 - 21 x^3 - 4 x^2 + 24 x - 35\\\\6(x^4-(21)/(6)* x^3-(4)/(6)* x^2+4 x-(35)/(6))`

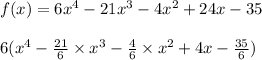
By Rational root Theorem ,factors of the above expression can be

`\text{Factors of 35,factors of 6,and factors of }(35)/(6)=\pm 1,\pm 5,\pm 7, \pm 35,\pm 2,\pm 3, \pm 6`

`,\pm (1)/(2),\pm(1)/(3),\pm (1)/(6),\pm(5)/(2),\pm(5)/(3),\pm(5)/(6),\pm(7)/(2),\pm(7)/(3),\pm(7)/(6),\pm(35)/(2),\pm(35)/(3),\pm(35)/(6)`

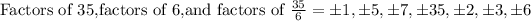
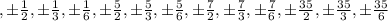
That is , by observing at the options, the factors of the given expression could be

`x=\pm (7)/(2)\\\\ \text{and}, x=\pm (7)/(3)`

Substituting these four Values one by one in the Polynomial function

`f((7)/(2))=6 * ((7)/(2))^4 -21 * ((7)/(2))^3 -4 * ((7)/(2))^2 +24 * ((7)/(2))-35\\\\ f((7)/(2))=900.375 -900.375 - 49+84-35\\\\f((7)/(2))=0`

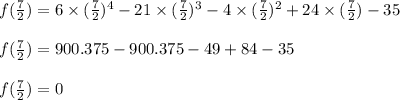
As,we have to find single factor,you will find that,

`f((-7)/(2))\\eq 0 \text{and} f((\pm7)/(3))\\eq 0.`

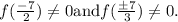
So,
`x=(7)/(2)\\\\ 2x-7`

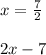
is the factor of the polynomial.

Option A: 2 x -7