Step 1
The given equation is

Required: To find the real zeroes by factorization and the turning points.
Step 2
Find the number of real zeroes
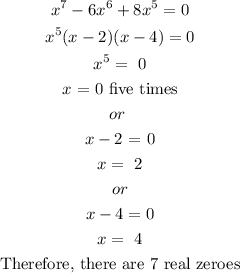
Step 3
Find the number of turning points.
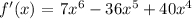
![\begin{gathered} As\text{ se}en\text{ from the differential, the number of turning points is found by subtracting 1 from the highest power of the function.} \\ \text{Hence, the number of turning points = 7-1 = 6} \\ \text{There are 6 turning points} \end{gathered}]()
Therefore, there are 7 real zeroes and 6 turning points; 0, 2 and 4
The answer is option A