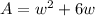Question

A rectangle's length is 6 units greater than its width. Write an equation expressing the rectangle's area, A, as a function of w. A) A = 2w + 6 B) A = 4w + 12 C) A = w2 + 6w D) A = w2 + 12w

Answer 1

I hope this helps you



length =width +6


Area=width × length



Area=w. (w+6)

Answer 2

Option C is correct.

an equation expressing the rectangle's area ,
`A = w^2+6w`

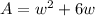
Explanation

Area of rectangle(A) is given by:

`A = lw`

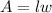
where,

l is the length of the rectangle and w is the width of the rectangle.

As per the statement:.

A rectangle's length is 6 units greater than its width

⇒
`l = 6+w`

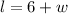
Substitute in the above formula;a we have;

`A = (6+w) \cdot w`

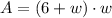
Using distributive property we have;

`A = 6w+ w^2`

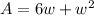
or

`A = w^2+6w`

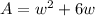
Therefore, an equation expressing the rectangle's area is,
`A = w^2+6w`