Question

Mike and Beatrice purchase a house for $200,000. If the equation V = 200,000(1.03)x represents the value of the house after x years, how many years will it take the house to be worth approximately $225,000?

A) 4 years
B) 5 years
C) 6 years
D) 7 years

Answer 1

225000=200000(1.03^t)

9/8=1.03^t

ln(9/8)=tln(1.03)

t=ln(9/8)/ln(1.03)

t=3.98

t=4 years

Answer 2

Option A - 4 years

Explanation:

Given : Mike and Beatrice purchase a house for $200,000. If the equation
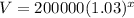`V = 200000(1.03)^x` represents the value of the house after x years.

To find : How many years will it take the house to be worth approximately $225,000?

Solution :

The given equation is
`V = 200000(1.03)^x`

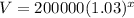
x is the number of years and V is the price of house.

In how many years the price became $225,000

V=$225,000

Substitute in the equation,

`V = 200000(1.03)^x`

`225000 = 200000(1.03)^x`

`(225000)/(200000)=(1.03)^x`

`1.125=(1.03)^x`

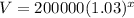
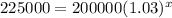
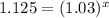
Taking log both side,

`\log(1.125)=\log((1.03)^x)`

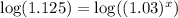
Apply logarithmic formula,
`\log(a)^x=x\log(a)`

`\log(1.125)=x\log(1.03)`

`(\log(1.125))/(\log(1.03))=x`

`3.98=x`

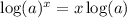
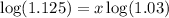
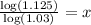
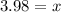
Approximately x=4 years.

Therefore, Option A is correct.