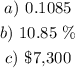
Firstly, we have to write the general depreciation fomula as follows;
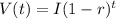
where V(t) represents the value of the commodity after a certain t years
I is the initial value of the item
r is the annual percentage change (rate of depreciation)
t is the number of years
a) Here, we want to calculate the annual rate of change
According to the data given in the question;
V(t) = $13,000
I = $41,000
r = ?
t = 2004-1994 = 10 years
Now, we proceed to substitute these values, to find the find of r as follows;
![\begin{gathered} 13,000=41,000(1-r)^(10) \\ (1-r)^{10\text{ }}\text{ = }(13,000)/(41,000) \\ (1-r)^{10\text{ }}=\text{ }(13)/(41) \\ \\ (1-r)\text{ = }\sqrt[10]{(13)/(41)} \\ \\ 1-r\text{ = 0.8915} \\ r\text{ = 1-0.8915} \\ r\text{ = 0.1085} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/6tglmvumsgsc7zbd8v14.png)
b) To write r in percentage form, we have to multiply the answer in 'a' above by 100
We have this as ;
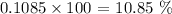
c) Here, we want to get the car value by year 2009
In that instance;
V(t) = ?
I = $41,000
r = 0.1085
t = 2009-1994 = 15
Substituting these values, we have;
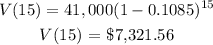
To the nearest 50 dollars, this is $7,300