Answer: 95
Explanation:
Let x be the random variable that represents the weight of the students.
Given :
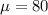 and
and
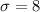 .
.
Using formula :
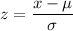
Also, the weight of the students is normally distributed.
Z-score corresponds to x= 64
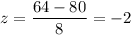
Z-score corresponds to x= 96
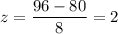
The probability that the students weigh between 64 and 96 pounds:
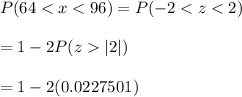 [using z-table for right tailed test]
[using z-table for right tailed test]
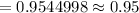
Out of 100 students, the number of students weigh between 64 and 96 pounds :
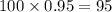
Hence, the umber of students weigh between 64 and 96 pounds =95