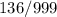case a) the repeating decimal is 36
Let
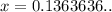
Multiply x by a power of
 , one that keeps the decimal part of the number the same:
, one that keeps the decimal part of the number the same:

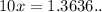
Subtract
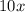 from
from
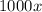
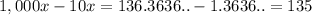
The repeating decimals should cancel out
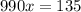
solve for x
Divide by
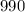 both sides
both sides
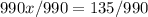

Simplify
Divide by
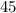 both numerator and denominator
both numerator and denominator
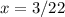
therefore
the answer case a) is
The fraction in simplest form is
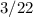
case b) the repeating decimal is 136
Let
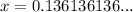
Multiply x by a power of
 , one that keeps the decimal part of the number the same:
, one that keeps the decimal part of the number the same:
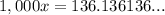
Subtract
 from
from
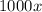
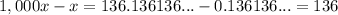
The repeating decimals should cancel out
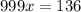
solve for x
Divide by
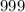 both sides
both sides
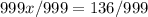
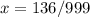 -----> irreducible
-----> irreducible
therefore
the answer case b) is
The fraction in simplest form is