Question

Jamal wants to install a rectangular 2025 cm² window in his garden shed. That area of window comes in several length/width combinations, and he wants to minimize the perimeter to prevent drafts. What is the least perimeter possible for the window?

Answer 1

The ideal size will be a 45cmx45cm square, giving you a perimeter of 180cm.

Explanation:

The shortcut answer here is that the square will always be the most efficient rectangle for border to area, so the sides should be the square root of 2025 cm, or 45 cm each, giving you a total of 180 minimum perimeter.

The full solution is to express the perimeter as a function of the length and width, define either length or width as a function of the other, take the entire expression's derivative and solve for zero. Let's do it:

So first the area:

2025 = wl

l = 2025 / w

Now the sides:

`p = 2w + 2l\\p = 2w + 2(2025 / w)\\p = 2w + 4050 / w`

Then we can take its derivative with respect to w

`p = 2w + 4050(1)/(w)\\(dp)/(dw) = 2 + 4050(-1)/(w^2)\\`

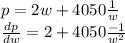
Now we can set the derivative to zero, and solve for w:

`(dp)/(dw) = 2 + 4050(-1)/(w^2)\\0 = 2 + (-4050)/(w^2)\\-2 = (-4050)/(w^2)\\2w^2 = 4050\\w^2 = 2025\\w = √(2025)\\w = 45`

So the width being 45, we can get the length by dividing the area by that amount, which of course is also 45.