The secant function is the reciprocal of the cosine function.
We can evaluate trigonometric functions of angles outside the first quadrant using reference angles as we have already done with the sine and cosine functions. The procedure is the same:
Find the reference angle formed by the terminal side of the given angle with the horizontal axis. The trigonometric function values for the original angle will be the same as those for the reference angle, except for the positive or negative sign, which is determined by x– and y-values in the original quadrant. (Figure) shows which functions are positive in which quadrant.
An even function is one in which f(-x) = f(x)
An even function is one in which f(-x) = - f(x)
Cosine and secant are even:
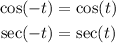
Therefore from the drop down the correct answer : secant function is EVEN