The half-range sine series is the expansion for
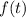
with the assumption that
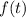
is considered to be an odd function over its full range,

. So for (a), you're essentially finding the full range expansion of the function
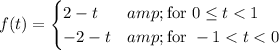
with period 2 so that
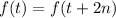
for

and integers

.
Now, since
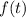
is odd, there is no cosine series (you find the cosine series coefficients would vanish), leaving you with
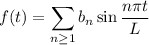
where
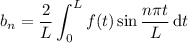
In this case,
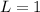
, so
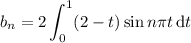
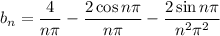
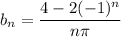
The half-range sine series expansion for
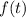
is then
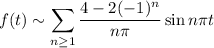
which can be further simplified by considering the even/odd cases of

, but there's no need for that here.
The half-range cosine series is computed similarly, this time assuming
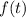
is even/symmetric across its full range. In other words, you are finding the full range series expansion for
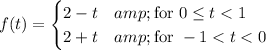
Now the sine series expansion vanishes, leaving you with
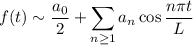
where
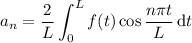
for
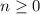
. Again,
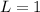
. You should find that
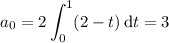
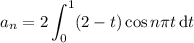
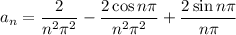
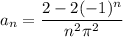
Here, splitting into even/odd cases actually reduces this further. Notice that when

is even, the expression above simplifies to

while for odd

, you have
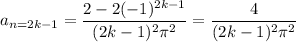
So the half-range cosine series expansion would be
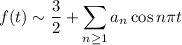
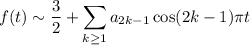
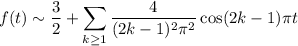
Attached are plots of the first few terms of each series overlaid onto plots of
. In the half-range sine series (right), I use

terms, and in the half-range cosine series (left), I use
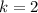
or
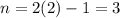
terms. (It's a bit more difficult to distinguish
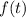
from the latter because the cosine series converges so much faster.)