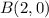we know that
If a point is a solution of the inequality
then
The point must satisfy the inequality
we have
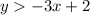
The solution of the inequality is the shaded area above the dotted blue line
see the attached figure to better understand the problem
Step 1
Point
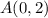
Substitute the value of x and the value of y in the inequality
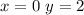
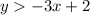
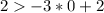
 -------> is not true
-------> is not true
therefore
The point A is not a solution for the inequality
See the attached figure------> the point A is not on the shaded area
Step 2
Point
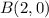
Substitute the value of x and the value of y in the inequality
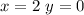
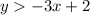
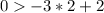
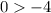 -------> is true
-------> is true
therefore
The point B is a solution for the inequality
See the attached figure------> the point B is on the shaded area
Step 3
Point
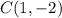
Substitute the value of x and the value of y in the inequality
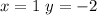
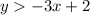
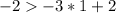
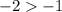 -------> is not true
-------> is not true
therefore
The point C is not a solution for the inequality
See the attached figure------> the point C is not on the shaded area
Step 4
Point

Substitute the value of x and the value of y in the inequality
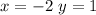
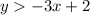

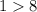 -------> is not true
-------> is not true
therefore
The point D is not a solution for the inequality
See the attached figure------> the point D is not on the shaded area
the answer is