Question

Which set of side lengths is a Pythagorean triple?

A.2, 3, 13
B.5, 7, 12
C.10, 24, 29
D.11, 60, 61

Answer 1

Answer: The correct option is (D). 11, 60, 61.

Step-by-step explanation: We are to select the correct set of side lengths that makes a Pythagorean triple.

To make a Pythagorean triple, the lengths of the three sides of a triangle must satisfy the following relation.

Hypotenuse² = base² + perpendicular².

i.e., the square of the length of the largest side must be equal to the sum of the squares of the lengths of the two smaller sides.

Option (A) is 2, 3, 13.

We have

`2^2+3^2=4+9=13\\eq 13^2.`

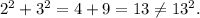
So, this option is not correct.

Option (B) is 5, 7, 12.

We have

`5^2+7^2=25+49=74\\eq 12^2.`

So, this option is not correct.

Option (C) is 10, 24, 29.

We have

`10^2+24^2=100+576=676\\eq 29^2.`

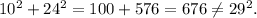
So, this option is not correct.

Option (D) is 11, 60, 61.

We have

`11^2+60^2=121+3600=3721=61^2.`

So, this option is correct.

Thus, the set of side lengths that makes a Pythagorean triple is 11, 60, 61.

Thus, (D) is the correct option.