Question

The points A(-3,-4) and B(5,0) form a line segment. Find the coordinates of the point P that partitions segment AB in a 2:3 ratio. O (0.2, 10.4) O (0.2,-2.4) O (7.2, 10.4) O (7.2,-2.4)

Answer 1

To find the coordinates of the point P on a line segment AB in ratio 2:3, use the next formula:

`P=(\frac{nx_1+mx_2_{}}{m+n},(ny_1+my_2)/(m+n))`

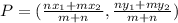
Where m:n represents the ratio of 2:3

m =2 and n=3

Replace these values using

A(-3,-4) = (x1,y1)

B(5,0) = (x2,y2)

`P=(((3)(-3)+(2)(5))/(2+3),((3)(-4)+(2)(0))/(2+3))`
`P=((-9+10)/(5),(-12+0)/(5))`
`P=((1)/(5),(-12)/(5))`

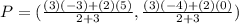
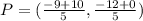
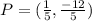
Therefore:

`P=(0.2,-\text{ }2.4)`

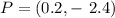
So, the correct answer is the second option (0.2,-2.4)