To find the coordinates of the point P on a line segment AB in ratio 2:3, use the next formula:
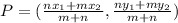
Where m:n represents the ratio of 2:3
m =2 and n=3
Replace these values using
A(-3,-4) = (x1,y1)
B(5,0) = (x2,y2)
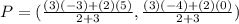
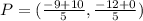
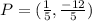
Therefore:
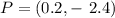
So, the correct answer is the second option (0.2,-2.4)