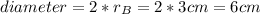Question

Cylinders A and B are congruent. Cylinder A has a volume of 27π cm3 and a height of 3 cm. What is the diameter of Cylinder B?

Answer 1

V = πR²h = π*R²*3
27π = 3πR²
R² = 9
R = 3

Diameter = 3*2 = 6cm

Answer 2

diameter = 6 cm

Explanation:

Two cylinders are congruent when they have the same size and dimensions. In that respect, it is possible to use mathematical criteria for determining the previous statement as follows;

If the cylinder A and B are congruent, then the volume is equivalent to

`V_A=V_B`

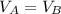
Reminding the volume of the cylinder can be determined by

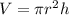`V=\pi r^2h`, where r is the radius of the cylinder and h the height. With the given data from the problem, it substitutes the values as follows,

`27cm^3=(3cm)*  \pi r_(B)^2`

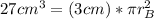
To determine the diameter of the cylinder B is necessary to calculate its radius, thus;

`r_(B)^2=(27cm^3)/((3cm)*  \pi) \\ \sqrt{r_(B)^2} =\sqrt{(27cm^3)/((3cm)*  \pi)}  \\r_(B)=3 cm`

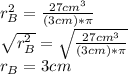
Reminding the radius of the cylinder corresponds to the radius of any circle of which the diameter is the double of its radius, then

`diameter = 2*r_(B)= 2* 3cm=6cm`