(x+1)²- 8
1) Considering the equation 2x²+4x-6, and that in the expression (x-h)²+k
we have:
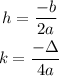
2) Then, let's find out h and k the values of the vertex of that quadratic function:

So the vertex is (-1, -8). Plugging into that 2nd expression, we'll have an equivalent one:
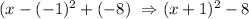
3) So the equivalent expression to that quadratic equation is (x+1)²-8