Question

ex lorn 3. An expression is given 2x2 + 4x - 6 Determine the values of h and k that make the expression (x - h)2 + k equivalent to the given expression. Identify the vertex and the zeros or roots! 6 . 3 I

Answer 1

(x+1)²- 8

1) Considering the equation 2x²+4x-6, and that in the expression (x-h)²+k

we have:

`\begin{gathered} h=(-b)/(2a) \\ k=(-\Delta)/(4a) \end{gathered}`

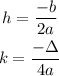
2) Then, let's find out h and k the values of the vertex of that quadratic function:

`\begin{gathered} h=(-4)/(2(2))=(-4)/(4)=-1 \\ k=(-\Delta)/(4(2))=(-(4^2-4(2)(-6)))/(8)=(-64)/(8)=-8 \end{gathered}`

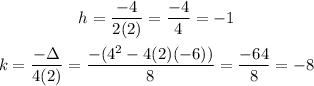
So the vertex is (-1, -8). Plugging into that 2nd expression, we'll have an equivalent one:

`(x-(-1)^2+(-8)\text{ }\Rightarrow(x+1)^2-8`

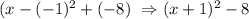
3) So the equivalent expression to that quadratic equation is (x+1)²-8