Question

Suppose a bag contains 8 white chips and 2 black chips. What is the probability of randomly choosing a white chip, not replacing it, and then randomly choosing another white chip?

A. 1/25
B. 28/45
C. 1/45
D. 16/25

Answer 1

probability of choosing a white chip : 8/10 reduces to 4/5
not replacing
probability of picking another white chip : 7/9

probability of both : 4/5 * 7/9 = 28/45 <==

Answer 2

Answer: B. 28/45

Explanation:

Since, Given numbers of white chips = 8,

Black chips = 2,

Total chips = 8 + 2 = 10,

Thus, the probability of white chip in first drawn =
`(8)/(10)`

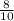
Now, after replacing one white chip,

Remaining white chips = 8 - 1 = 7,

Total remaining chips = 10 - 1 = 9,

Thus, the probability of white chip in second drawn =
`(7)/(9)`

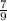
Hence, the probability of randomly choosing a white chip, not replacing it, and then randomly choosing another white chip,

= The probability of white chip in first drawn × The probability of white chip in second drawn

`=(8)/(10)* (7)/(9)`

`=(56)/(90)=(28)/(45)`

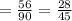
⇒ Option B is correct.