Question

Arrange the steps to solve this system of linear equations in the correct sequence.

x + y = -2
2x – 3y = -9

A. Subtract 3x + 3y = -6 (obtained in step 1) from 2x – 3y = -9 (given) to solve for x.

B) Substitute the value of x in the first equation (x + y = -2) to get y = 1.

C) The solution for the system of equations is (-3, 1).

D) x = -15

E) The solution for the system of equations is (-15, 13).

F) Add 3x + 3y = -6 (obtained in step 1) to 2x – 3y = -9 (given), and solve for x.

G) x = -3

H) Substitute the value of x in the first equation (x + y = -2) to get y = 13.

J) Multiply the first equation by 3: 3(x + y) = 3(-2) 3x + 3y = -6.

Basically put them in order. Please?

Answer 1

J Multiply the first equation by 3
F Add the two equations and solve for x
G x = -3
B Substitute the value of x in the first equation, y = 1
C the solution is (-3, 1)

Answer 2

Answer: The answer is given below.

Step-by-step explanation: The given system of linear equations is :

`x+y=-2,~~~~~~~~~~~~~~(i)\\\\2x-3y=-9.~~~~~~~~~~~(ii)`

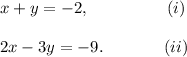
Multiplying equation (i) by 3, we have

`3(x+y)=3*(-2)\\\\\Rightarrow 3x+3y=-6.~~~~~~~~~~~~~~~(iii)`

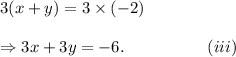
Adding equations (ii) and (iii), we get

`5x=-15\\\\\Rightarrow x=-3.`

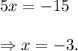
Substituting the value of 'x' in equation (i), we get

`-3+y=-2\\\\\Rightarrow y=1.`

Thus, the solution set is (-3, 1).

Therefore, the correct steps in ascending order to solve the above system of equations are given below:

Step 1: (J) Multiply the first equation by 3: 3(x + y) = 3(-2) ⇒ 3x + 3y = -6.

Step 2: (F) Add 3x + 3y = -6 (obtained in step 1) to 2x – 3y = -9 (given), and solve for x.

Step 3: (G) x = -3.

Step 4: (B) Substitute the value of x in the first equation (x + y = -2) to get y = 1.

Step 5: (C) The solution for the system of equations is (-3, 1).