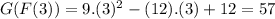Question

If F(x) = 3x - 2 and G(x) = x^2 + 8, What is G(F(x))?

Answer 1

G(F(x)) = (3x - 2)^2 + 8 = (9x^2 - 12
x + 4) + 8 Remove parentheses.

G(F(x)) = 9x^2 - 12x + 4 + 8


Add like terms.

G(F(x)) = 9x^2 - 12x + 12

Answer 2

`G(F(x))=9x^(2)-12x+12`

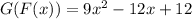
Explanation:

Given two functions G(x) and F(x) to obtain the composing function G(F(x)) or F(G(x)) we need to replace in one expression the variable ''x'' by the entire expression of the function which is between brackets.

For example, to obtain F(G(x)) given

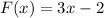`F(x)=3x-2` and

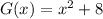`G(x)=x^(2)+8` given that G(x) is between brackets, the expression
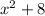`x^(2)+8` will act as the variable ''x''.

Therefore,

`F(G(x))=3(x^(2)+8)-2`

`F(G(x))=3x^(2)+22`

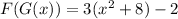
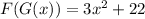
In the exercise, to obtain G(F(x)) , the expression
`3x-2` of F(x) will act as the variable ''x''

`G(F(x))=(3x-2)^(2)+8`

`G(F(x))=9x^(2)-12x+4+8`

`G(F(x))=9x^(2)-12x+12`

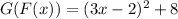
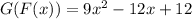
For example If we want to obtain
`G(F(3))`

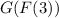
We first find
`F(3)` :

`F(3)=(3).(3)-2=7`

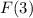And then we replace in the expression of G(x)

`G(7)=7^(2)+8=57`

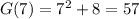
Or either replace x = 3 in the expression of the composing function G(F(x)) :

`G(F(3))=9.(3)^(2)-(12).(3)+12=57`