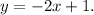Question

The equation of the line is perpendicular to y= 1/2X +3 and passes through -2 and 5 in slope intercept form

Answer 1

Step-by-step explanation

The slope-intercept equation of a line has the form

`y=m\cdot x+b,`

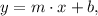
where m is the slope of the line and b is its y-intercept.

Now, there is a very interesting relationship between the slopes (m_1 and m_2) of perpendicular lines:

`m_1=-(1)/(m_2)\text{.}`

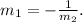
Looking at the given equation, we can say that its slope is 1/2. Then,

`m=-(1)/((1)/(2))=-2.`

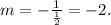
Then, our desired equation becomes

`y=-2x+b\text{.}`

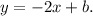
Now, we know that our line passes through (-2,5). This means that

`5=-2\cdot(-2)+b\text{.}`

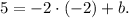
Solving this equation for b, we get

`\begin{gathered} 5=4+b, \\ 4+b=5, \\ b=5-4, \\ b=1. \end{gathered}`

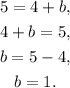Answer

The desired line has equation

`y=-2x+1.`