Answer:
The width and length of the rectangle are
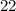 and
and
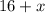 , for
, for
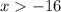 , respectively.
, respectively.
Explanation:
From Geometry, we remember that area of the rectangle (
 ) is defined by:
) is defined by:
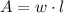 (1)
(1)
Where:
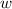 - Width.
- Width.
 - Length.
- Length.
In addition, we know that area is described by a first-order polynomial:
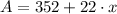 (2)
(2)
Meaning that is the product of another first-order polynomial and a constant. That is:
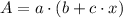 (3)
(3)
Now we determine the Great Common Divisor of 352 and 22:
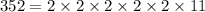
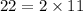
The Great Common Divisor is 22.
Then, the area of the rectangle can be expressed by this expression:
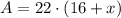 (3b)
(3b)
According to this, the width and length of the rectangle are
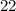 and
and
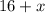 , for
, for
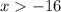 , respectively.
, respectively.