Answer:
44 years.
Explanation:
Let original amount be 100.
We have been given that the half life of Pb-210 is 22 years. A decayed animal shows 25% of the original Pb-210 remains.
We will use half-life formula to solve our given problem.
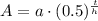 , where,
, where,
A = Amount after t units of time,
a = Initial amount,
t = Time,
h = Half-life.

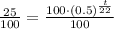
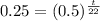
Take natural log of both sides:

Using natural log property
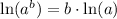 , we will get:
, we will get:
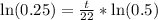
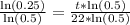


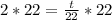
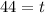
Therefore, the animal has been deceased to 44 years.