Question

In problem 7-14 your class constructed a large tetrahedron like the one at right. Assume the dimensions of the shaded tetrahedron at right are half of the dimensions of the similar enlarged tetrahedron.A. If the volume of the large tetrahedron is 138 in.3, find the volume of the small shaded tetrahedron.B. Each face of a tetrahedron is an equilateral triangle. If the small shaded tetrahedron has an edge length of 16 cm, find the total surface area for each of the tetrahedra.

Answer 1

We have two similar tetrahedrons, where the shaded has dimensions that are half the dimensions of the large tetrahedron.

A. For scaled figures, the volume is affected by the cube of the scale factor.

This means that if the dimensions are half the original dimensions, the volume will be 0.5³ = 0.125 times the original volume.

Then, if the volume of the large tetrahedron is 138 in³, then the volume of the shaded tetrahedron is:

`V_(sh)=((1)/(2))^3V=0.125*138=17.5\text{ in}^3`

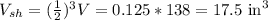
B. In the case of the areas, the area of a scaled figure will be affected by the square of the scale factor.

We have to calculate the area for both tetrahedrons.

The shaded tetrahedron has edge lengths of 16 cm. Then, we can calculate his total surface as four times the area of a face, as we have four equal faces per tetrahedron.

We then start by calculating the area of an equlateral triangle with side 16 cm.

We can draw this figure to help with the calculations:

We now that the area of a triangle is half the product of the base and the height, so we calculate the height as:

`\begin{gathered} h^2=16^2-8^2 \\ h^2=256-64 \\ h^2=192 \\ h=√(192) \\ h=8√(3) \end{gathered}`

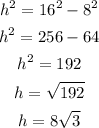
Now we can calculate the area of the triangle as:

`A_t=(b*h)/(2)=(16*8√(3))/(2)=64√(3)`

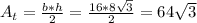
Then, the area of the shaded tetrahedron is:

`A_(sh)=4*A_t=4*64√(3)=256√(3)`

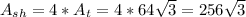
We can now calculate the area of the large tetrahedron, which has edges of length 2*16 = 32 cm.

We can start calculating the height again:

`\begin{gathered} h^2=32^2-16^2 \\ h^2=1024-256 \\ h^2=768 \\ h=√(768) \\ h=16√(3) \end{gathered}`

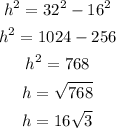
We can now calculate the area of a face as:

`A_t=(b*h)/(2)=(32*16√(3))/(2)=256√(3)`

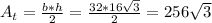
and the total surface of the large tetrahedron as:

`A=4*A_t=4*256√(3)=1024√(3)`

We can now compate the ratio between areas:

`(A_(sh))/(A)=(256√(3))/(1024√(3))=(1)/(4)=((1)/(2))^2`

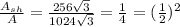
We can see that the areas are related by the square of the scale factor.

Answer:

A. The volume of the shaded tetrahedron is 17.5 in³.

B. The surface of the shaded tetrahedron is 256√3 cm².

The surface of the large tetrahedron is 1024√3 cm².