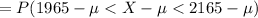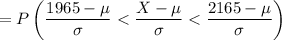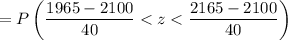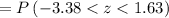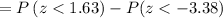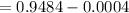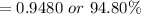Answer:
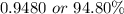
Explanation:
The life expectancy of a typical light bulb is normally distributed with a mean of 2,100 hours and a standard deviation of 40 hours.
So, here,
μ = mean = 2100,
σ = standard deviation = 40,
We know that,
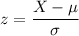
We have to calculate the probability that a light bulb will last between 1,965 and 2,165 hours.
i.e