Question

During the Labor Day weekend, Amy and Kathleen each ran in a race. Amy ran in a 5K and completed it in 31 minutes and 15 seconds. Kathleen ran in a half-marathon, which is 21.1 kilometers, and completed it in 2 hours, 11 minutes, and 52.5 seconds.

Let d represent distance in kilometers, r represent the rate, and t represent time in minutes. The proportional relationship

Answer 1

velocity=distance/time

a=5/(31*60+15)=5/1875=1/375

k=21.1/(2*3600+11*60+52.5)=21.1/7912.5=1/375

a=k

The both ran at the same speed.

(1km/375s)(3600s/h)=9.6km/h

Answer 2

The relationship is rate is same.

Explanation:

Given : During the Labor Day weekend, Amy and Kathleen each ran in a race. Amy ran in a 5K and completed it in 31 minutes and 15 seconds. Kathleen ran in a half-marathon, which is 21.1 kilometers, and completed it in 2 hours, 11 minutes, and 52.5 seconds.

Let d represent distance in kilometers, r represent the rate, and t represent time in minutes.

To find : The proportional relationship ?

Solution :

We know,
`r=(d)/(t)`

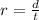
1 hour = 60 minutes = 60 × 60 seconds

First we find the rate of both Amy and Kathleen.

Amy ran in a 5 km and completed it in 31 minutes and 15 seconds.

Rate of Amy in km/hr is given by,

`r_1=(5)/((31)/(60)+(15)/(60* 60))`

`r_1=(5)/(0.516+0.00416)`

`r_1=(5)/(0.52016)`

`r_1=9.6km/hr`

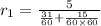
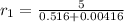
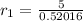
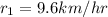
Kathleen ran in a half-marathon, which is 21.1 kilometers, and completed it in 2 hours, 11 minutes, and 52.5 seconds.

Rate of Kathleen in km/hr is given by,

`r_2=(21.1)/(2+(11)/(60)+(52.5)/(60* 60))`

`r_2=(5)/(2+0.18333+0.014583)`

`r_2=(5)/(2.197)`

`r_2=9.6km/hr`

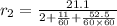
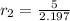
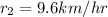
Both man ran at the same speed.

Therefore, The relationship is rate is same.