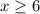Question

Solve for xx and graph the solution on the number line below. If possible, resolve your answer to a single inequality. In case of no solution (\varnothing∅), leave the number line blank.2>-x+3 and −x+3≤−3

Answer 1

We are given the following two inequalities.

`2>-x+3\; \; and\; \; -x+3\le-3`

Let us solve each of the above inequalities

`\begin{gathered} 2>-x+3 \\ 2-3>-x \\ -1>-x \\ 11 \end{gathered}`

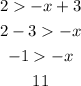
Please note that the direction of inequality is reversed whenever we multiply/divide or shift the variables to other sides.

Now, let us solve the other inequality.

`\begin{gathered} \; -x+3\le-3 \\ \; -x\le-3-3 \\ \; -x\le-6 \\ x\ge6 \end{gathered}`

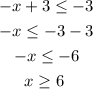
So, the two solutions are x > 1 and x ≥ 6

Substitute each of the above solutions into the original inequalities and check if they satisfy the inequalities or not.

`\begin{gathered} For\; x>1\text{:} \\ 2>-1+3 \\ 2>2\; (\text{not satisfied)} \\ -x+3\le-3 \\ -1+3\le-3 \\ 2\le-3\text{ (not satisfied)} \end{gathered}`

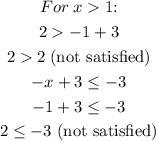
Since the x > 1 do not satisfy the inequalities, our solution is x ≥ 6

`\begin{gathered} \text{For}\; x\ge6\colon \\ 2>-x+3 \\ 2>-6+3 \\ 2>-3\; (\text{satisfied)} \\ \; -x+3\le-3 \\ \; -6+3\le-3 \\ \; -3\le-3\; (\text{satisfied)} \end{gathered}`

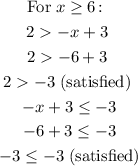
Finally, let us graph the solution on the number line.

The solution is all the values of x equal to or greater than 6.

`x\ge6`