Question

Two researchers are studying the decline of orangutan populations. In one study, a population of 784 orangutans is expected to decrease at a rate of 25 orangutans per year. In a second study, the population of a group of 817 orangutans is expected to decrease at a rate of 36 per year. After how many years will the two populations be the same?

Answer 1

Step 1:
Set Variables (We will use x & y)

x = years
y = total orangutan population

Step 2:
Set up Equations

784 - 25x = y
817 - 36x = y

Step 3:
Set equations equal to each other & solve

784 - 25x = 817 - 36x
784 = 817 - 11x
-33 = -11x
3 years = x

Answer 2

The answer is 3 years.

Explanation:

Let the years be denoted by 't' ,when both populations will be same.

1st study says a population of 784 orangutans is expected to decrease at a rate of 25 orangutans per year.

Equation becomes:

`y=784-25t`

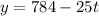
In a second study, the population of a group of 817 orangutans is expected to decrease at a rate of 36 per year.

Equation becomes:

`y=817-36t`

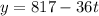
Now to solve for 't' we will equal both the equations.

`784-25t=817-36t`

`36t-25t=817-784`

`11t=33`

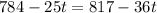
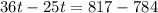
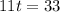
So, t = 3 years.

So, the answer is 3 years.