Question

A triangle has one side that measures 1 feet and another side that measures 20 inches. What is the possible length for the third side?

Answer 1

For any given triangle. The sum of two sides must be greater than the length of the third side.

This means, with two sides given as 20 inches and 12 inches (1 foot = 12 inches), we can conclude that;

`\begin{gathered} 20+12>x \\ \text{Where } \\ x=\text{third side of the triangle} \end{gathered}`

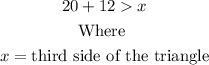
From this inequality we can now deduce the following;

`\begin{gathered} 20+12>x \\ 32>x \\ \text{That is, } \\ x<32 \end{gathered}`

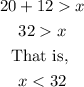
Alo, we have;

`\begin{gathered} x+12>20 \\ \text{Note that the sum of two sides must be greater than the third side} \\ x>20-12 \\ x>8 \end{gathered}`
`\begin{gathered} x+20>12 \\ x>12-20 \\ x>-8 \end{gathered}`

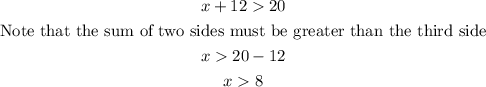
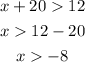
The length of the third side cannot be a negative number, hence we shall disregard the third option, that is x > -8.

Therefore, the possible length for the third side shall be

`\begin{gathered} x<32,x>8 \\ OR \\ 32>x>8 \end{gathered}`

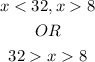
The possible length of the third side shall be either

Less than 32 inches

OR

Greater than 8 inches