We use the formula for compound growth to figure this problem out. Formula is:
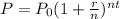
Where,
- P is the future value
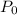 is the initial deposite
is the initial deposite- r is the rate of interest annually
- n is the number of times compounding occurs (n=1 for annual compounding, n=2 for semiannual compounding etc.)
- t is time
Given P=15,000, r=5%=0.05 (in decimal), n=1 (since annual compounding), and t=5 years, we can solve:
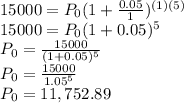
So, Trisha Long needs to deposit $11,752.89 today in the account.
ANSWER: $11,752.89