Question

A rock that had been dropped from a high platform is moving with a kinetic energy of 180 J when it strikes the ground. Ignore air resistance. What kinetic energy did the rock have when it had fallen one-third of the distance to the ground?

Answer 1

`E_T = E _k_i_n + E_p_o_t = constant`

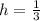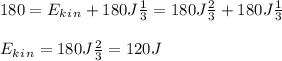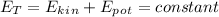
The total energy of the rock does not change.

Let h be the ratio between the height of the rock and H, so that the height of the rock = H·h.
The energy of the rock that has been dropped from a height H just before it hits the ground with h = 0:


`E_T= 180J + mgH \ h = 180J + mgH \ 0 = 180J + 0`

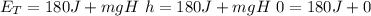
The energy of the rock when it is released from rest from height H with h = 1 :


`E_T = E_k_i_n + mgH = 0 + mgH = 180J`

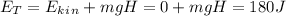
so:
`mgH = 180J`

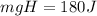
You find:


`E_T = E_k_i_n + 180J \ h = 180`

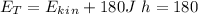
for
`h = (1)/(3)`


`180 = E_k_i_n + 180J (1)/(3) = 180J (2)/(3) + 180J (1)/(3) \\ \\ E_k_i_n = 180J (2)/(3) = 120J`

Answer 2

180 J = (-9.8)x

x = -18.36 m

(1/3)(-18.36)= -6.12 m

(-9.8)(-6.12) = 60 J