I assume
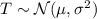
refers to a random variable
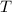
following a
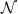
ormal distribution with mean
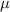
and variance
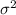
.
Recall that the moment generating function for a random variable
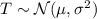
is
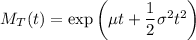
and that the moment generating function for a linear combination of random variables is equivalent to the product of each individual random variables moment generating functions; that is, if
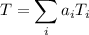
, then
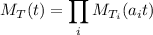
So you have
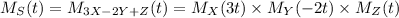
with

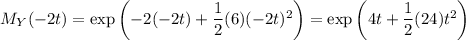

which means
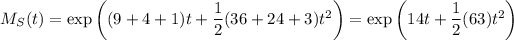
This is the moment generating function of yet another normal distribution, so that

, with expectation 14 and variance 63.