Answer:
a)
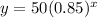
Explanation:
Let the function that shows the given situation is,
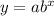
Where a and b are any unknown numbers,
By the given diagram,
When x = 1, y = 42.5,
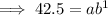
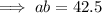 ------(1)
------(1)
Again, when x = 4, y = 26,
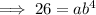
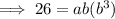
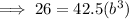 ( By equation (1) )
( By equation (1) )
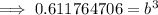
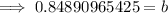
Again, By equation (1),
a = 50.0642203646
Hence, the equation that shows the given graph,
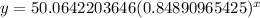
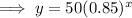
⇒ Option a is correct.