Question

Find an equation of the tangent line to the curve 2(x^2+y^2)2=25(x^2−y^2) (a lemniscate) at the point (3,1)

Answer 1

`\bf \left[ 4x^3+2\left[ 2xy^2+x^22y(dy)/(dx) \right]+4y^3(dy)/(dx) \right]=25\left[x-y(dy)/(dx) \right] \\\\\\ 4x^3+4xy^2+4x^2y(dy)/(dx)+4y^3(dy)/(dx)+25y(dy)/(dx)=25x \\\\\\ \cfrac{dy}{dx}[4x^2y+4y^3+25y]=25x-4x^3+4xy^2 \\\\\\ \cfrac{dy}{dx}=\cfrac{25x-4x^3+4xy^2}{4x^2y+4y^3+25y}\impliedby m=slope`

notice... a derivative is just the function for the slope

now, you're given the point 3,1, namely x = 3 and y = 1

to find the "m" or slope, use that derivative, namely
`f'(3,1)=\cfrac{25x-4x^3+4xy^2}{4x^2y+4y^3+25y}`

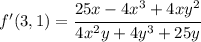
that'd give you a value for the slope

to get the tangent line at that point, simply plug in the provided values
in the point-slope form


`\bf y-{{ y_1}}={{ m}}(x-{{ x_1}})\qquad \begin{cases} x_1=3\\ y_1=1\\ m=slope \end{cases}\\ \qquad \uparrow\\ \textit{point-slope form}`

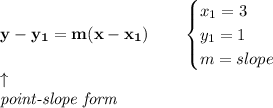
and then you solve it for "y", I gather you don't have to, but that'd be the equation of the tangent line at 3,1