Given data:
Mass of rock 1;
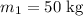
Height rock 1 lifted;
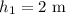
Mass of rock 2;
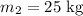
Height rock 2 lifted;
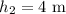
The work done in lifting the rock is given as,
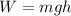
Here, m is the mass of the rock, g is the acceleration due to gravity (g=10 m/s²) and h is the height the rock lifted.
The work done in lifting rock 1 is given as,
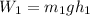
Substituting all known values,
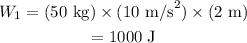
The work done in lifting rock 2 is given as,
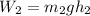
Substituting all known values,

On comparing the work done in lifting rock 1 and 2 we conclude that,
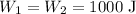
Therefore, the same amount of work is done in lifting a 50 kg rock by 2 meters and lifting a 25 kg rock by 4 meters.