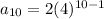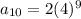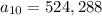Question

Find the 10th term of the following geometric sequence: 2, 8, 32, 128.        A. 164,357   B. 621,325   C. 524,288   D. 248,221

Answer 1

common ratio = 8/2 = 32/8 = 4

10th term = a1*r^(n - 1) where a1 = 2 , r = 4 and n = 10
= 2 * 4^9
= 524,288

Answer 2

`524,288`

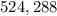
Explanation:

Find the 10th term of the following geometric sequence

2, 8, 32, 128.......

To find the nth term of any geometric sequence we use formula

`a_n=a(r)^(n-1)`

Where 'a' is the first term and 'r' is the common ratio

To find common ratio we divide the second term by first term

`(8)/(2) =4`

`(32)/(8) =4`

`(128)/(32) =4`

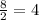
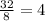
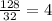
`r=4` and
`a=2`

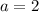
Plug in the values in the formula, n=10

`a_n=a(r)^(n-1)`

`a_(10)=2(4)^(10-1)`

`a_(10)=2(4)^(9)`

`a_(10)= 524,288`