Question

Determine if triangle EFG and triangle HIJ are or are not similar, and, if they are, state how you know. (Note that figures are NOT necessarily drawn to scale.)

Answer 1

Given the triangles EFG and HIJ, you can identify that:

`EG=19\text{ }`
`EF=18`
`\begin{gathered} FG=16\text{ } \\ \\ \text{ }HI=90 \\ \\ IJ=80 \end{gathered}`
`\begin{gathered} m\angle F=67\text{ \degree} \\ \\ m\angle I=67\text{ \degree} \end{gathered}`

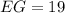
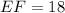
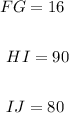
By definition, two triangles are similar if the lengths of the corresponding sides are in proportion and their corresponding angles are congruent.

In this case, you can identify that you know two pairs of corresponding sides. Then, you can find in they are in proportion. Set up that:

`(EF)/(HI)=(FG)/(IJ)`

Substituting values and simplifying, you get:

`\begin{gathered} (18)/(90)=(16)/(80) \\ \\ (1)/(5)=(1)/(5) \end{gathered}`

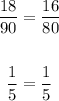
Notice that they are in proportion.

You can also identify that the corresponding angles F and I are congruent because they have equal measure.

Therefore, since you know that two sides are proportionate and the included angles are congruent, you can conclude that the triangles are similar, based on the Side-Angel-Side Theorem (SAS).

Hence, the answer is: Third option.