Question

Find the standard form of the equation of the parabola with a focus at (0, 4) and a directrix at y = -4.

Answer 1

y=1/16 x^2

Explanation:

vertex= (0,0)

vertex--> focus=p=4

(use the graph start at the vertex and stop at the focus which is (0,4) )

(x-0)^2=4p(y-0) --> x^2=4(4)(y-0) --> x^2/16=16y/16 --> y=x^2/16 or y=1/16x^2

Answer 2

so... hmm notice the picture below

keep in mind that, the vertex is always half-way between the directrix and the focus point, because the focus point and the directrix are both a distance "p" from the vertex, just in opposite directions, but the same distance "p" to either

so.. from the picture, notice the length of "p"

and keep in mind that, based on the position of the focus point and the directrix, we know the parabola is vertical and opening upwards

that means that the "x" variable is the squared variable
thus, we use this vertex form, here in the rectangle


`\bf \begin{array}{llll} (y-{{ k}})^2=4{{ p}}(x-{{ h}}) \\ \boxed{(x-{{ h}})^2=4{{ p}}(y-{{ k}})}\\ \end{array} \qquad \begin{array}{llll} vertex\ ({{ h}},{{ k}})\\ {{ p}}=\textit{distance from vertex to }\\ \qquad \textit{ focus or directrix} \end{array}`

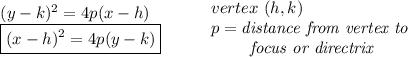
well, you know what "p" is, and what h,k are, so just plug them in